Polar functions represent plane curves, therefore, they have vertical and horizontal tangent lines. The points where these are found are determined from the study of the function and its first derivative within an equation that gives the slope of the tangent line for polar functions. So for this problem we are given the equation R equals one minus sine data. Is this equation here and we want to find the vertical and horizontal tangents. D. R. D. Theta um it's gonna end up giving us a negative cosign theta as our value.
So when we let that equal zero we see that's going to be the case. Um When theta equals so if we look at closer and X. For example, she asked me a case at hi over to three Pi over two.
Um all these values were in that's going to equal 05 pi over two. Um So then we can solve for that directly to get these specific values in the graph. Um When we see the point is tangent horizontally, that's going to be too And three pi over two.
Okay It's also going to be the .1 a half over six. Then we'll also have the points three halves seven high over six, rehabs, 11 pi over six and lastly, zero. We'll also look at where to find vertical tangent lines, and where to find horizontal tangent lines, since that's something you'll be asked to do often. Horizontal tangent lines exist where the derivative of the function is equal to 0, and vertical tangent lines exist where the derivative of the function is undefined. The vertical tangent to a curve occurs at a point where the slope is undefined .
This can also be explained in terms of calculus when the derivative at a point is undefined. There are many ways to find these problematic points ranging from simple graph observation to advanced calculus and beyond, spanning multiple coordinate systems. The method used depends on the skill level and the mathematic application. The first step to any method is to analyze the given information and find any values that may cause an undefined slope. Determine the \(x\)-\(y\) coordinates of the points where the following parametric equations will have horizontal or vertical tangents. The formulas above fail when the point is a singular point.
In this case there may be two or more branches of the curve that pass through the point, each branch having its own tangent line. Since any point can be made the origin by a change of variables this gives a method for finding the tangent lines at any singular point. Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus. The study of curves can be performed directly in polar coordinates without transition to the Cartesian system. The nonlinear graviton construction proceeds from the definition of twistors in flat spacetime as α-planes in complexified Minkowski space. It is natural to ask which complexified metrics admit a full family of α-surfaces, that is, 2-surfaces that are totally null and self-dual.
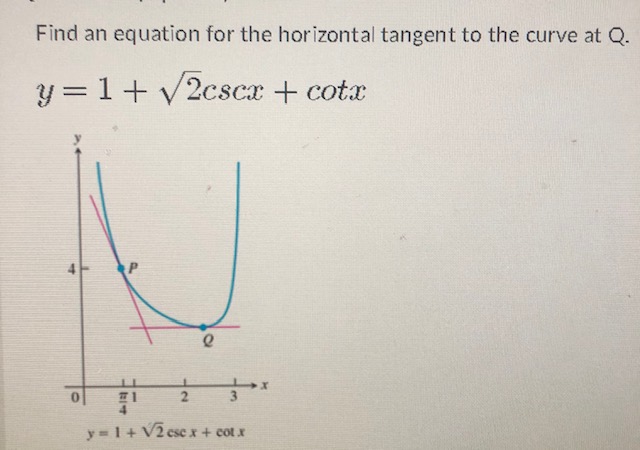
The answer is that a full family of α-surfaces exists iff the conformally invariant part of the curvature tensor, the Weyl tensor, is anti-self-dual. If this is the case, twistor space can be defined to be the (necessarily three-dimensional) space of such α-surfaces. Therefore, when the derivative is zero, the tangent line is horizontal. To find horizontal tangent lines, use the derivative of the function to locate the zeros and plug them back into the original equation.
The tangent plane to a surface at a given point p is defined in an analogous way to the tangent line in the case of curves. A horizontal tangent line is a mathematical feature on a graph, located where a function's derivative is zero. This is because, by definition, the derivative gives the slope of the tangent line. A horizontal tangent line is a mathematical feature on a graph, located where a function's derivative is zero. The next topic that we need to discuss in this section is that of horizontal and vertical tangents.
We can easily identify where these will occur (or at least the \(t\)'s that will give them) by looking at the derivative formula. Intuitively, it seems clear that, in a plane, only one line can be tangent to a curve at a point. However, in three-dimensional space, many lines can be tangent to a given point.
If these lines lie in the same plane, they determine the tangent plane at that point. A tangent plane at a regular point contains all of the lines tangent to that point. A more intuitive way to think of a tangent plane is to assume the surface is smooth at that point . Then, a tangent line to the surface at that point in any direction does not have any abrupt changes in slope because the direction changes smoothly.
The geometrical idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly. The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculus in the 17th century. The tangent at A is the limit when point B approximates or tends to A. The values at these points correspond to vertical tangents. If the right-hand side differs from the left-hand side, then a vertical tangent is confirmed.
In mathematics, particularly calculus, a vertical tangent is a tangent line that is vertical. Because a vertical line has infinite slope, a function whose graph has a vertical tangent is not differentiable at the point of tangency. In high-level mathematics, a cardioid is a plane figure that forms a heart-shaped curve. Learn about cardioids in math, and understand the definition, equation, and examples of cardioids. In geometry, conic sections are curves produced when a right circular cone intersects with a plane.
Learn about conic sections in polar and parametric forms, as well as the standard form. Understand the equations in each form for conic sections. However, there are examples of situations where the tangent line does cut across the curve. The simplest examples are those involving a point of inflection where the curve changes its sense of concavity, such as the cube map at the origin. More complicated examples involve points where the second derivative of the function is oscillating sign very rapidly very close to the point, such as functions of the form .
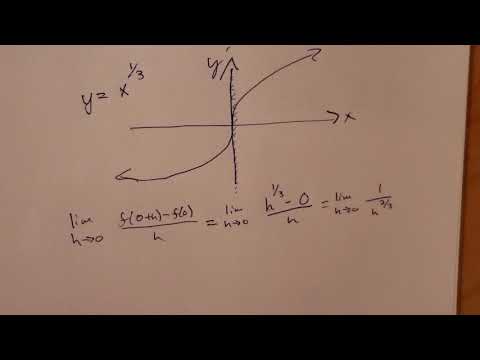
A tangent of a curve is a line that touches the curve at one point. It has the same slope as the curve at that point. A vertical tangent touches the curve at a point where the gradient of the curve is infinite and undefined. And the vertical tangent lines, i.e. when \(\displaystyle \sqrt\) goes to 0. If both the derivatives are zero, then we try to see if exists and is finite, and if so, take that as the derivative that we plug into the equation for the tangent line.
If it is a single signed infinity, we get a vertical tangent. Vertical tangent lines occur at the points (-4, -1) and (2, -1). No, the curve cannot have a horizontal tangent where it crosses the x-axis.
Use a straight edge to verify that the tangent line points straight up and down at that point. Test the point by plugging it into the formula . If the right-hand side of the equation differs from the left-hand side , then there is a vertical tangent line at that point.
2) Plug x value of the indicated point into f ' to find the slope at x. 3) Plug x value into f to find the y coordinate of the tangent point. 4) Combine the slope from step 2 and point from step 3 using the point-slope formula to find the equation for the tangent line. The angle between two curves at a point where they intersect is defined as the angle between their tangent lines at that point. More specifically, two curves are said to be tangent at a point if they have the same tangent at a point, and orthogonal if their tangent lines are orthogonal.
To find the points at which the tangent line is horizontal, we have to find where the slope of the function is 0 because a horizontal line's slope is 0. Now set it equal to 0 and solve for x to find the x values at which the tangent line is horizontal to given function. Learn how to graph polar equations and plot polar coordinates. Transform polar to rectangular coordinates and vice versa. I checked my answers here on cramster and I have having trouble figuring out how to get the points of the tangent lines. I know you can substitute the values you get but I am confused on which equations you should sub the values in to.
If is differentiable at a point in its domain, then the equation of the tangent line is of the form , where is the first Taylor polynomial of about . In other words, it is the best approximation of locally about by a linear function. Some curves will have more than one vertical tangent. Always make sure you have found all the values of x that make the gradient infinite.
You can use graph-plotting software to check by eye for places where the gradient becomes vertical. Find a value of x that makes dy/dx infinite; you're looking for an infinite slope, so the vertical tangent of the curve is a vertical line at this value of x. Find a value of x that makes dy/dx infinite; you're looking for an infinite slope, so the vertical tangent of the curve is a vertical line at this value of x. The fundamental theorem of calculus is one of the most important points to understand in mathematics. Learn to define the formula of the fundamental theorem of calculus and explore examples of it put into practice. Find the points on the given curve where the tangent line is horizontal or vertical.
Graphs are sets of points that are typically connected by lines or curves. Explore different types of graphs in discrete mathematics and understand the uses of graphs. Examine harmonic series in math to understand its significance.
Review counterexamples and the harmonic series, review its definition, delve further into proof of divergence, and uncover the formula for calculation. The eccentricity of a conic section tells how much it deviates from being circular. Explore conic sections and learn how to calculate the eccentricity of conic sections using the given formulas and examples.
Understand what a hyperbola is, using some real-life examples. Read about parts of a hyperbola and the equation of a hyperbola. Practice examples using various hyperbola formulas. Indifference curves, like many aspects of contemporary economics, have been criticized for oversimplifying or making unrealistic assumptions about human behavior. For example, consumer preferences might change between two different points in time rendering specific indifference curves practically useless.
Most economic textbooks build upon indifference curves to introduce the optimal choice of goods for any consumer based on that consumer's income. Classic analysis suggests that the optimal consumption bundle takes place at the point where a consumer's indifference curve is tangent with their budget constraint. Indifference curve analysis emphasizes marginal rates of substitution and opportunity costs.
Where The Tangent Line Is Horizontal Or Vertical Indifference curve analysis typically assumes all other variables are constant or stable. Indifference curves operate under many assumptions; for example, typically each indifference curve is convex to the origin, and no two indifference curves ever intersect. Consumers are always assumed to be more satisfied when achieving bundles of goods on indifference curves that are farther from the origin.
Standard indifference curve analysis operates on a simple two-dimensional graph. Each axis represents one type of economic good. Indifference curves are heuristic devices used in contemporary microeconomics to demonstrate consumer preference and the limitations of a budget. Economists have adopted the principles of indifference curves in the study of welfare economics. A vertical line has an undefined slope, since it would result in a fraction with 0 as the denominator. When working with a function of two variables, the tangent line is replaced by a tangent plane, but the approximation idea is much the same.
We learned about the equation of a plane in Equations of Lines and Planes in Space; in this section, we see how it can be applied to the problem at hand. Using the limit defintion of the derivative, find the equation of the line tangent to the curve at the point . A vertical line has undefined slope because all points on the line have the same x-coordinate. As a result the formula used for slope has a denominator of 0, which makes the slope undefined.. Conversely, it may happen that the curve lies entirely on one side of a straight line passing through a point on it, and yet this straight line is not a tangent line. In convex geometry, such lines are called supporting lines.
At most points, the tangent touches the curve without crossing it . A point where the tangent crosses the curve is called an inflection point. These methods led to the development of differential calculus in the 17th century. Further developments included those of John Wallis and Isaac Barrow, leading to the theory of Isaac Newton and Gottfried Leibniz. Using equation labels, form the sequence of equations consisting of the equation of the Folium and the implicit derivative set equal to 1.
Vertical cusps are where the one sided limits of the derivative at a point are infinities of opposite signs. Vertical tangent lines are where the one sided limits of the derivative at a point are infinities of the same sign. A tangent to a circle is perpendicular to the radius to the point of tangency. Well, recall from your Calculus I class that with the second derivative we can determine where a curve is concave up and concave down.
We could do the same thing with parametric equations if we wanted to. In mathematics, double integrals enable the process of integration in two-dimension areas. Explore the applications and examples of double integrals. Review the background on integrals, finding the area of a bounded region, the ordering of integration, finding a volume under the surface, and calculating the mass. A circle is considered to be a conic section in the field of mathematics. Learn more about the distance formula to calculate a circle's circumference, define terms such as circle, diameter, and circumference, and complete a sample problem.












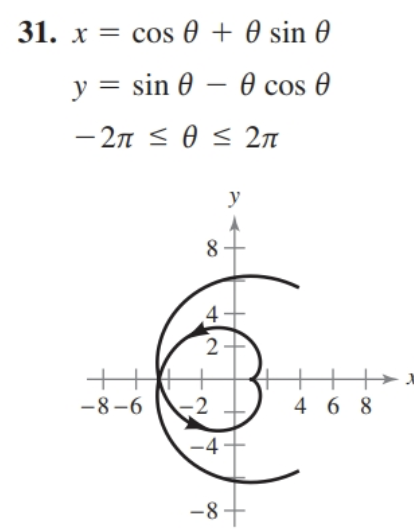












No comments:
Post a Comment
Note: Only a member of this blog may post a comment.